Fotografiando asteroides con un radar

Mi último artículo trataba de una secuencia fotográfica obtenida de un asteroide por medio de un radar. Creo que sería interesante aclarar como se realizan estas fotografías, para lo que me basaré en un didáctico artículo de Emily Lakdawalla, publicado en su blog (The Planetary Society).

Un radar es un sistema activo que emite una señal de radio y espera a recibir su eco para chequear si existe algún objeto en su radio de acción. La velocidad de las ondas de radio es constante y conocida (igual a la velocidad de la luz), por lo que basta con disponer de un reloj preciso para calcular la distancia a la que se encuentra, que es la mitad del espacio que puede recorrer la luz en el tiempo medido (porque tiene que ir y volver).

Si disponemos de un radar lo suficientemente potente, podemos dirigirlo hacia la ubicación conocida de un asteroide y ver lo que pasa. Gráficamente sería algo así:

El radar emite un pulso , que llega al asteroide y rebota sobre la superficie “visible” desde el radar. La señal que llegue a la parte más adelantada del asteroide rebotará antes que la que llega a la parte central.

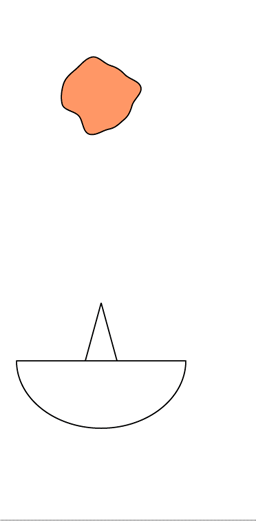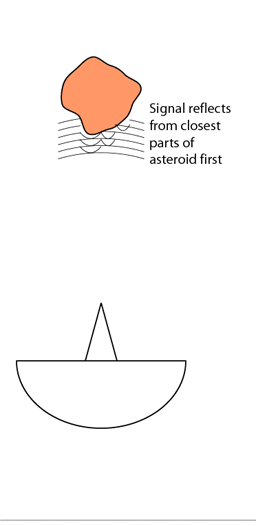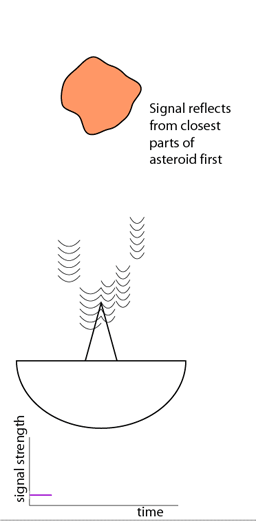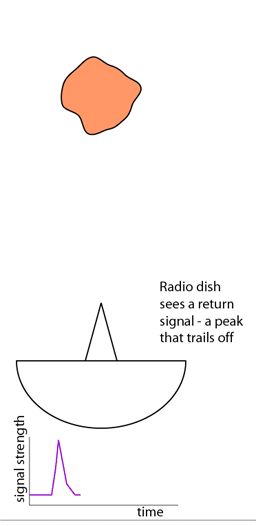
La señal recibida en tierra es la que se muestra en la parte inferior de la animación. No proporciona mucha información. A lo sumo, el tamaño del asteroide, que será la velocidad de la luz dividido entre el tiempo que transcurre desde que se empieza a recibir el eco hasta que deja de percibirse. Y, asumiendo que el cuerpo es aproximadamente simétrico, ese valor  hay que multiplicarlo por dos, ya que se corresponde con el tamaño sólo del hemisferio visible, quedando toda la mitad posterior en sombra.

La forma descrita por la curva de intensidad recibida también proporciona información. Si asciende progresivamente, significa que tiene forma de punta. Si llega abruptamente y luego queda un remanente, significa que tiene una forma más cilíndrica.

Pero hay otras maneras más inteligentes de utilizar el radar, basadas en el efecto Doppler. Permitidme que explique brevemente en que consiste este efecto, para que todo el mundo pueda seguir el resto del artículo. Es muy sencillo y consiste en el cambio de frecuencia de una onda provocado por el movimiento del emisor. Aunque pueda parecer un poco complicado enunciándolo así, viendo este vídeo se aclararán todos los conceptos.

Aplicando el efecto Doppler a un radar, podemos identificar las partes que se mueven y a qué velocidad.

Si consideramos que todos los cuerpos del sistema solar giran, se podría hacer un radar que aprovechase este efecto aplicándolo a la observación de asteroides.

Prosiguiendo con el ejemplo enunciado antes, si emitimos un pulso dirigido hacia un asteroide, que se desplaza por el espacio y además gira, obtenemos que la señal nos llega a la tierra con una frecuencia desplazada por ambos movimientos.

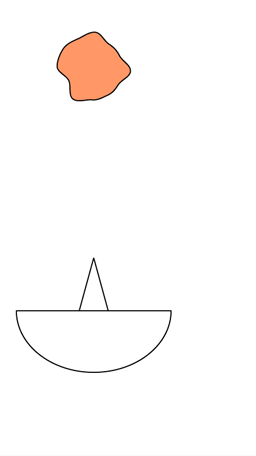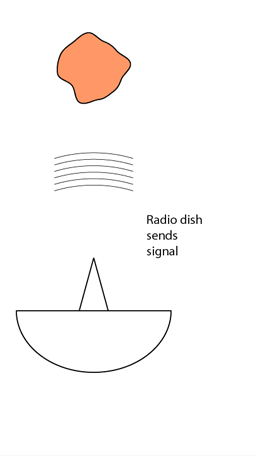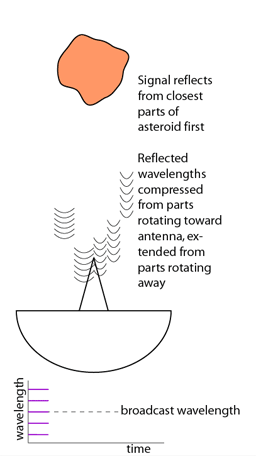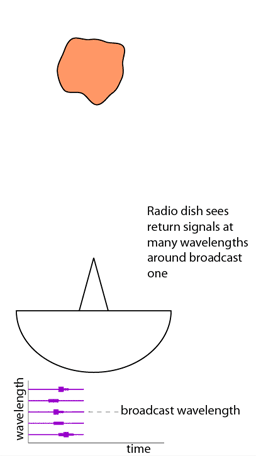
Si conocemos la velocidad a la que viaja el asteroide, se puede prever el desfase “ideal” que tendría la señal originado por el movimiento de traslación. De esta manera podemos aislar el desfase producido por el movimiento de giro, que es el que nos interesa. La parte del asteroide que gira hacia nosotros, nos devolverá una señal más comprimida (con frecuencia mayor a la emitida) y la que gira alejándose de nosotros devolverá una señal elongada (con frecuencia menor). Gráficamente sería algo así:

En la parte inferior de la animación, podemos ver cómo se muestrean las señales recibidas en diferentes longitudes de onda, que determinarán la resolución en metros de la fotografía (range-gate). Cada una de ellas recibe un eco similar al de la primera animación, pero de los puntos que se mueven con respecto a nosotros a la misma velocidad. Sería como una línea de la fotografía.

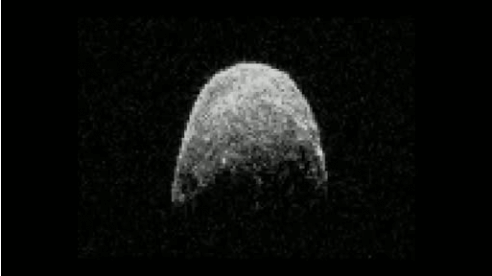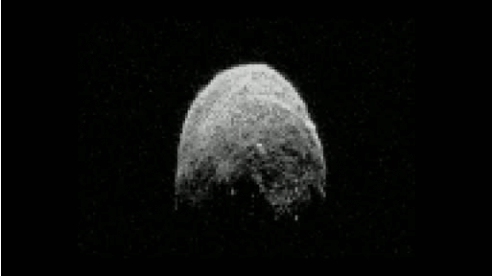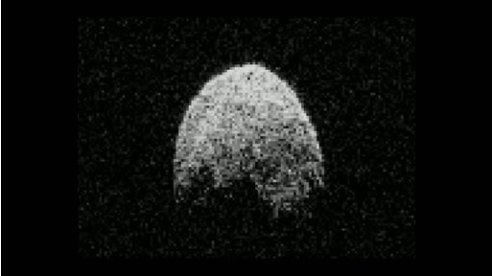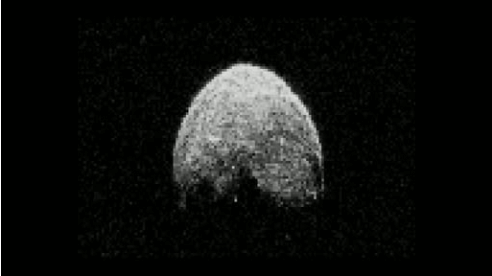
Un programa de ordenador procesa toda esta información (velocidad de movimiento, intensidad y distancia respecto al radar) para componer la representación gráfica del asteroide. Repitiendo a intervalos fijos este proceso, podemos crear la secuencia animada de la cabecera de la entrada.