Con π de pirámide
Hoy en día todavía hay mucha gente que cree que las pirámides fueron construidas por extraterrestres o atlantes. Los primeros cristianos y musulmanes creían que fue el propio Dios el que las creó. No hemos cambiado mucho en estos últimos siglos. Solo hemos remplazado una túnica por un traje espacial.
Un interesante argumento que apunta a que fue una inteligencia super avanzada la que diseñó las pirámides de la 4ª dinastía en Giza, es la presencia insolente del número [latex]\pi[/latex] en sus dimensiones, cuando según los egiptólogos, los egipcios no conocían los números reales, y solo se manejaban con fracciones de números enteros.
Recordemos que el número [latex]\pi[/latex] es el resultado de dividir el perímetro de una circunferencia entre su diámetro, y su valor es 3,1416.
¿Dónde aparece el número [latex]\pi[/latex] en las pirámides?
Los lados de la gran pirámide de Giza tienen las siguientes longitudes
- Lado Oeste: 230,357 m
- Lado Norte: 230,253 m
- Lado Este: 230,391 m
- Lado Sur: 230,454 m
Por lo tanto, el perímetro de la pirámide es:
P = 230,357 + 230,253 + 230,391 + 230,454 = 921,455 m
La altura de la pirámide es 146,5 m.
Si el perímetro de una circunferencia es:
P = 2 · [latex]\pi[/latex] · r
donde r es el radio, entonces
$latex \pi = { P \over 2 * r}$
Sustituyendo P por el perimetro de la pirámide y r por la altura obtenemos:
$latex \pi = {921,455 \over 2* 146,5} = 3,1449$
Una buena aproximación al número $latex \pi$, con un error de solo 3 milésimas. ¿Casualidad?
El papiro matemático de Rhind
Este papiro data del 1800 a.C. aproximadamente y contiene el enunciado y resolución de 87 problemas matemáticos, por lo que es un elemento valiosísimo para entender el nivel de conocimiento que tenían los egipcios en la época de las pirámides. En este papiro hay varios problemas interesantes, pero fijémonos ahora en el número 50. El enunciado del problema plantea cómo calcular el área de un círculo que tiene 9 unidades de diámetro (digamos metros). Para resolverlo se explica que hay que quitar 1/9 del diámetro y al resultado multiplicarlo por si mismo. El resultado es el mismo que el área del circulo.
Los egipcios tenían una curiosa manera de multiplicar. Por ejemplo para calcular el valor de 8 * 9, tomaban una de las dos cifras a multiplicar y hacían una tabla como la siguiente, en la que se duplicaba el valor en cada iteración
1…8 «
2…16
4…32
8…64 «
Como se quiere multiplicar por 9, tomamos los valores asociados al 8 y al 1 y los sumamos: 72 (que es 8×9)
En el problema que nos atañe, es incluso más fácil, ya que hay que tomar el valor asociado al 8: 64 $latex m^2$(8×8). El valor real de la superficie de la circunferencia es:
A = $latex \pi$ · $latex r^2$ = 63,6173 $latex m^2$
El resultado es bastante aproximado. Pero lo más inquietante es que en base a este método de cálculo se podría inferir un valor aproximado a $latex \pi$ expresado como fracción de números enteros:
a: área
d: diámetro
r: radio (2*r)=d
$latex a = (d-{d\over 9})^2$
$latex a= (d * (1- {1 \over 9}))^2$
$latex a= (d * {8 \over 9})^2$
$latex a= d^2 * {64 \over 81}$
$latex a= (2 * r)^2 * {64 \over 81}$
$latex a= 4 * r^2 * {64 \over 81}$
$latex a= r^2 * {256 \over 81}$
Según esta aproximación, los egipcios estaban aproximando a $latex \pi$ con la fracción $latex {256 \over 81}$ = 3,1605. ¿Otra coincidencia? Posiblemente si. Lo más seguro es que los egipcios empíricamente se hubiesen dado cuenta de que la aproximación detallada en el problema 50 del papiro de Rhind era lo suficientemente buena para darla por válida.
Si realmente hubiesen descubierto este factor constante en todas las circunferencias, no lo manejarían como $latex {256 \over 81}$, sino como fracciones de numerador igual a la unidad:
$latex {256 \over 81}$ = 3 + $latex {1 \over 9}$ + $latex {1 \over 27}$ + $latex {1 \over 81}$
Pero estas fracciones son muy incómodas de manejar en el sistema egipcio de multiplicación, pues todos los denominadores son impares, y ellos siempre trataban de evitarlos.
Explicaciones
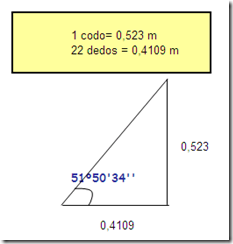
Una explicación sencilla a la presencia de $latex \pi$ en las proporciones de la gran pirámide es la manera en la que se construían. Por ejemplo, en los problemas 56 a 60 del papiro matemático de Rhind se enseña a calcular la pendiente de las paredes de una pirámide, lo que ellos conocían como seked. Para los egipcios el seked era la distancia en el plano horizontal que se desplaza la pared de la pirámide por cada codo que se levanta en altura. Un codo equivale aproximadamente a 0,523 metros. Un codo = 7 palmos y un palmo=4 dedos.
La pirámide de Keops tiene un seked de 22 dedos, o bien de 5½ palmos. Eso quiere decir que por cada codo que se eleva, pierde 5 palmos y medio en el plano horizontal.
Debido a la relación entre dedos y codo de 1 a 28, los egipcios podían construir con 28 sekeds distintos, desde 1, casi vertical, a 28 (45 grados). Todas las pirámides de Egipto están construidas con uno de estos sekeds, pero los mas comunes eran el 22, el 21, 19, 23 y 24. Hay alguna excepción que tiene un seked de más de 28 dedos, como la de Sneferu (30), con una inclinación algo menor de los 45º.
Los egipcios construían las pirámides desde fuera hacia dentro. Primero colocaban las piedras exteriores que eran cortadas con el seked de la pirámide, y luego se rellenaba el interior. Al llevar implícito este ángulo de inclinación de 51º 50’ 34”, por mera coincidencia se cumple lo expuesto en la primera parte de este artículo, al igual que ocurre en las pirámides de Huni y de Niuserra, y no ocurre por ejemplo en la de Micerinos, que tiene un seked de 23.
Hay otra teoría que a mi me gusta más (aunque no quiera decir que sea más plausible). Al medir la longitud de los lados de la pirámide normalmente habrían usado una cuerda, pero en distancias tan grandes como 230 metros, hasta las cuerdas más sólidas tienen cierta elasticidad. Es posible que en vez de utilizar una cuerda utilizasen una rueda para medir la longitud, con lo que se evitaría este problema. Imaginad una rueda cuyo diámetro sea un codo (0,523 m.) y por tanto su perímetro sea 1,643m. Para conseguir alcanzar los 230 metros de lado de la pirámide, debió de dar 140 giros completos. Si para calcular la altura se hubiesen estimado apilar tantos diámetros como el doble de giros dados por la rueda para dibujar el lado, entonces la altura sería 2 · 140 * 0,523m = 146,44m, exactamente la altura de la pirámide. En este caso también habría quedado grabada la impronta del número $latex \pi$ en las dimensiones de la pirámide, sin que los egipcios hubiesen tenido constancia de ello realmente.
Referencias:
http://www.3viajesaldia.com/el-misterio-de-pi-y-las-piramides-de-egipto/
http://www.egiptomania.com/jeroglificos/articulo/relaciones.htm
http://www.egiptologia.org/ciencia/matematicas/aritmetica_fracciones.htm

William Clavijo
21/09/16 14:32
439,922345154109 (Base Keops en codos) multiplicado por Pi/6 (Codo Real Egipcio: 0,5236) = 230,343 metros. Por favor lee el Libro del Estudio Original del Arqueólogo Ingles William Matthew Flinders Petrie). ahí encontrarás que el valor coincide exactamente.
Saludos
laverdadreal
23/05/17 17:40
Artículo insuficiente. Eligieron esas medidas al azar? Por qué son similares a la gran pirámide azteca? Como es posible la erosión acuática de la esfinge?. Porqué Mahmud Awass reconoce que los videntes acertaron en localizar «risibles» túneles que nadie quiere abrir? Conocían la masa terrestre? http://www.ancient-code.com/the-great-pyramid-of-giza-is-located-at-the-exact-center-of-earths-landmass/
Demasiadas preguntas sin resolver.